Applicant
Prof. Dr. Thorsten Pöschel
Institute for Multiscale Simulation
FAU Erlangen-Nürnberg
Project Summary
The implemented software extracts the continuum fields from discrete particle data. Many industrially relevant particulate systems are much larger than the typical particle size, i.e., they involve a large number of particles. To investigate these particulate systems it is, therefore, often neither possible nor necessary to consider information about the individual particles. In many cases a continuum description is sufficient or even desired – similar to the case of classical hydrodynamics, where one is not interested in the individual atoms or molecules, but rather in the macroscopic, hydrodynamic fields such as density, velocity, or stress. Similar to hydrodynamics, such continuous descriptions can be obtained for systems of macroscopic particles by averaging.
The developed software implements three conceptually different methods for this averaging process. The simplest ansatz is to assign each particle to the mesh cell containing its center of mass. In a more sophisticated approach, every particle is distributed to all intersecting cells according to the overlap volume between particle and cell. For this, the software makes use of an existing library for computing the intersection volume between spheres and tetrahedral (or hexahedral) mesh cells. In the third method, the position information is blurred by using Gauss distributions to represent the particles in space. Due to the typically large number of particles involved, the implementation employs distributed-memory parallelism.
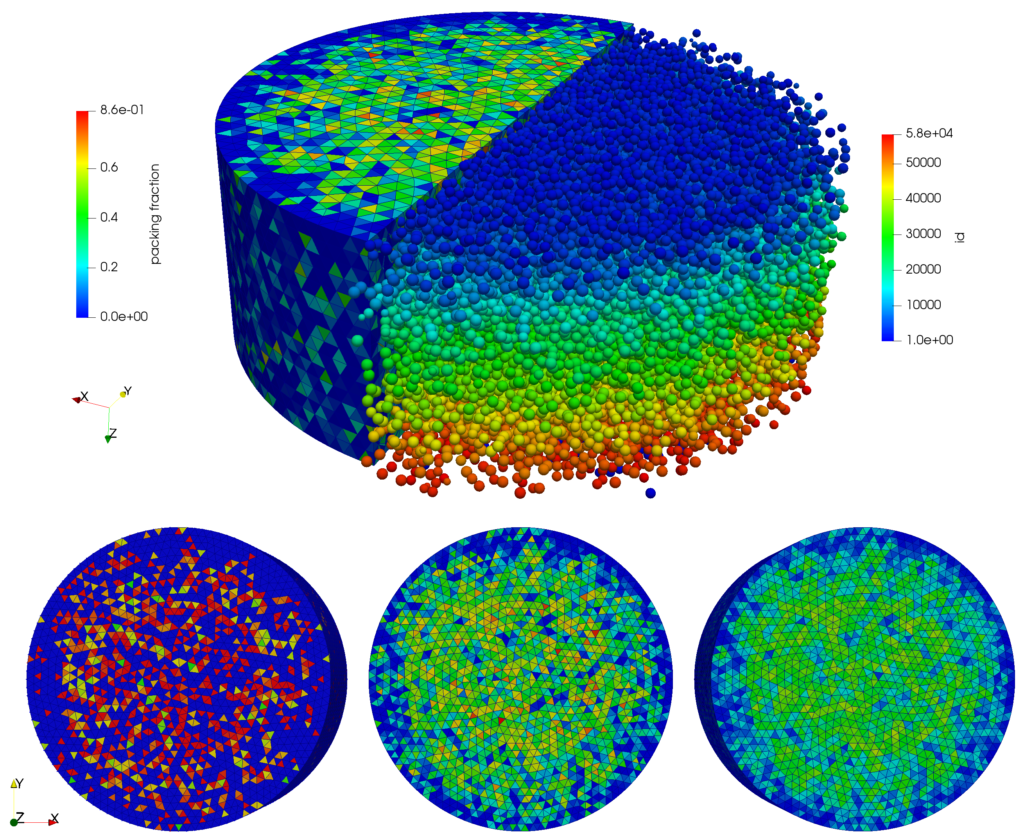
In the example depicted in Fig. 1, the packing fraction is computed in a static sphere packing, which priorly has been scanned using computer tomography. The packing has been generated by pouring polydisperse, spherical particles into a cylindrical container. Gravity points in negative z-direction. The mesh resolution is on the order of the particle size. Therefore, sorting based on the center of mass, which is shown on the bottom left in Fig. 1, leads to an insufficient result. Conversely, the other two methods yield more satisfactory results. Sorting based on the intersection volume resolves the packing fraction accurately on the mesh cells’ length scale while sorting based on Gaussian weights acts as a smoothing filter removing the finer details.

