Applicants
Prof. Dr. rer. nat. Ernst Rank
Technical University of Munich
PD. Dr rer. nat Ralf-Peter Mundani
University of Applied Sciences of the Grisons, Switzerland
PD. Dr.-Ing. habil. Stefan Kollmannsberger
Technical University of Munich
Project Overview
The project’s main objective was to enable transient large-scale image-based simulations using the Finite Cell Method (FCM). This was achieved by enhancing and extending AdhoC++, an in-house high-order FCM code which required dynamically changing FCM discretizations in distributed, parallel environments. To this end, the mesh data structures of AdhoC++ were optimized to allow for efficient dynamic mesh refinement of hp-refined meshes. Furthermore, the performance of the linear system solvers was improved by investigating the utilization of a multigrid solver specifically designed for the multi-level hp-refinement scheme. The primary benefit of this method lies in its ability to create distinct multigrid levels based on the refinement levels and polynomial orders of the elements which enables an elegant and straightforward multigrid solution by eliminating the necessity for grid transfer operators.
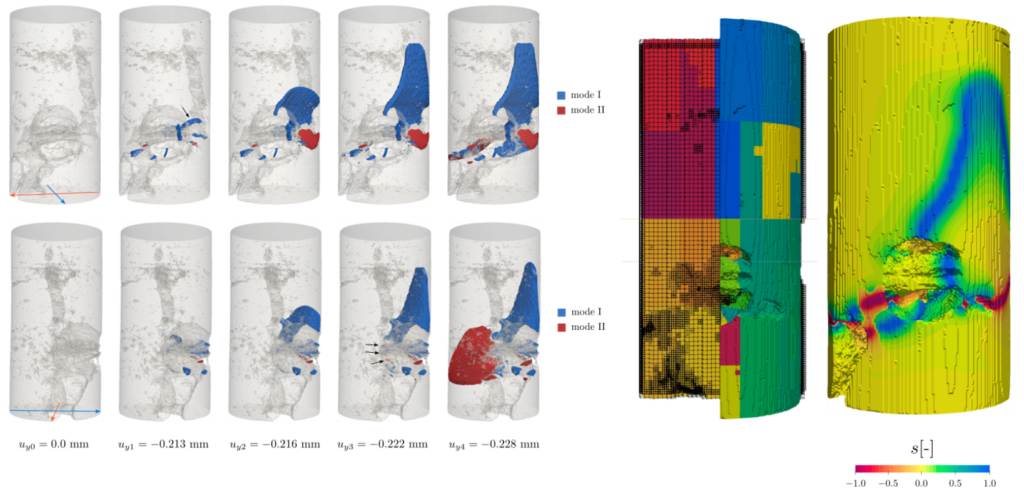
In a first step, quasi-static and transient simulations of heat transfer in selective laser melting were performed. Secondly, the parallel framework was extended to phase-field simulations of crack propagation in brittle materials. A number of alterations was necessary to solve the coupled and in general non-linear system of equations such as the introduction of an additional layer of ghost elements and an additional communication of refinement depths for the solution-based refinement strategy. Furthermore, a dynamic repartitioning strategy was implemented. In Figure 1, the fracture of a core sample taken 1500 m below the surface of Munich was simulated for the Geothermal Alliance Bavaria on the CoolMuc-2 using 96 processes on 48. The results were validated against experiments carried out at the Chair for Engineering Geology at TUM. We are grateful for the financial support from KONWIHR without which this work would not have been possible.
Publications
- Image-based material characterization of complex microarchitectured additively manufactured structures. N. Korshunova, J. Jomo, G. Lékó, D. Reznik, P. Balázs, S. Kollmannsberger. Computers & Mathematics with Applications, December 2020, Volume 8, Issue 11, Pages 2462-2480. https://doi.org/10.1016/j.camwa.2020.07.018
- Image-based numerical characterization and experimental validation of tensile behavior of octet-truss lattice structures, N. Korshunova, G. Alaimo, S.B. Hosseini, M. Carraturo, A. Reali, J. Niiranen, F. Auricchio, E. Rank, S. Kollmannsberger, Additive Manufacturing, May 2021, Volume 41, 101949. https://doi.org/10.1016/j.addma.2021.101949
- Bending behavior of octet-truss lattice structures: Modelling options, numerical characterization and experimental validation,i N. Korshunova, G. Alaimo, S.B. Hosseini, M. Carraturo, A. Reali, J. Niiranen, F. Auricchio, E. Rank, S. Kollmannsberger, Materials & Design, July 2021, Volume 205, 109693. https://doi.org/10.1016/j.matdes.2021.109693
- Hierarchical multigrid approaches for the finite cell method on uniform and multi-level hp-refined grids. J. Jomo, O. Oztoprak, F. de Prenter, N. Zander, S. Kollmannsberger and E. Rank. Computer Methods in Applied Mechanics and Engineering 386(1):114075, December 2021. https://doi.org/10.1016/j.cma.2021.114075
- Uncertainty quantification of microstructure variability and mechanical behavior of additively manufactured lattice structures. N. Korshunova, I. Papaioannou, S. Kollmannsberger and E. Rank. Computer Methods in Applied Mechanics and Engineering 385:114049, November 2021. https://doi.org/10.1016/j.cma.2021.114049
- Numerical evaluation of high cycle fatigue life for additively manufactured stainless steel 316L lattice structures: Preliminary considerations. G. Alaimo, M. Carraturo, N. Korshunova and S. Kollmannsberger. Material Design & Processing Communications Volume 3, number 4, August 2021. https://doi.org/10.1002/mdp2.249
- A three-field phase-field model for mixed-mode fracture in rock based on experimental determination of the mode II fracture toughness. L. Hug, M. Potten, G. Stockinger, K. Thuro, and S. Kollmannsberger. Engineering with Computers 38(6), July 2022. https://doi.org/10.1007/s00366-022-01684-9
- Predicting fracture in the proximal humerus using phase field models. L. Hug, G. Dahan, S. Kollmannsberger, E. Rank, and Z. Yosibash. Journal of the Mechanical Behaviour of Biomedical Materials 38(6), October 2022. https://doi.org/10.1016/j.jmbbm.2022.105415

