Applicant
Prof. Dr. Timothy Clark
Computer-Chemie-Centrum
FAU Erlangen-Nürnberg
Project Overview
EMPIRE is a newly conceived parallel semiempirical molecular orbital (MO) program that can treat as many as 1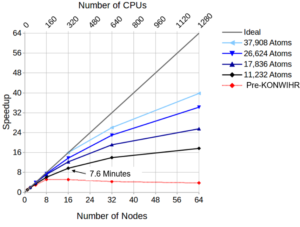
00,000 atoms on 4,000 cores or more. Within KONWIHR, performance enhancements in two areas have been achieved and an important step towards linear scaling made:
Diagonalization in self-consistent-field calculations: The distributed matrices (Hückel matrix for the initial guess and Fock matrix) have been redistributed from 1D stripes to 2D-block cyclic to give significantly improved diagonalization performance. The figure on the right shows the improvement achieved for complete self-consistent field (SCF) calculations on EMMY. Three different diagonalization library routines were investigated, the MKL routines PDSYEVR and PDSYEVD and the ELPA2 library (http://elpa.mpcdf.mpg.de/, which proves to be fastest and most effective.
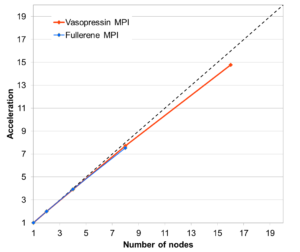
Harmonic frequencies: Calculating the normal vibrations of a system numerically is a trivially parallel task that, however, requires attention in order to achieve good load balancing. The EMPIRE implementation (shown for the example of ten OMP threads per CPU on EMMY) gives approximately 92% parallel efficiency, even for such small systems as vasopressin and C60-fullerene, as shown in the Figure on the right. This implementation involves two-level parallelism between and within the individual SCF/gradient calculations.
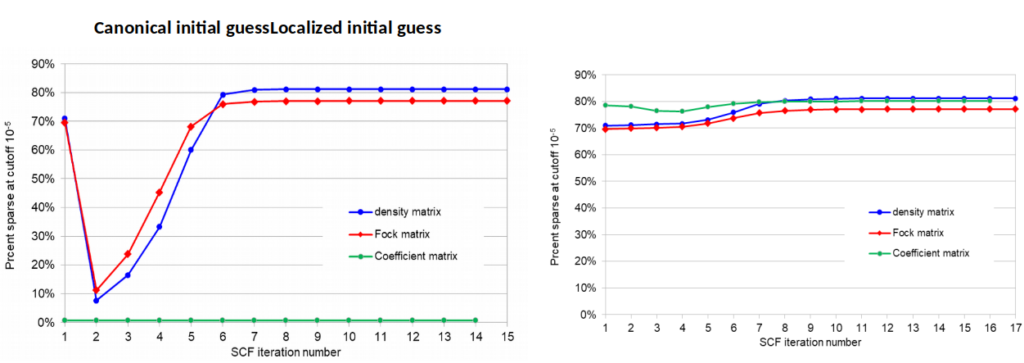
Matrix Sparseness: EMPIRE is not currently a linear-scaling code because it performs the full SCF-calculation in order to provide a standard for linear scaling approximations. We have conducted an investigation of the sparseness of the one-electron, density, Fock and MO-coefficient matrices as a preparation for using sparse matrix algorithms to approach linear scaling without sacrificing accuracy. At convergence, all but the coefficient matrix are sparse but this is not the case in the early SCF iterations (left plot below). Localizing the initial guess leads to far more sparse matrices (right plot) without changing the result. Currently, the localization technique used scales badly, is iterative and difficult to parallelize. It will therefore be replaced by a Cholesky factorization, which has none of these problems and provides orbitals that are almost as local. The way is then open to completely automatic close to linear scaling SCF calculations.
