Applicant
Prof. Dr. Eric Sonnendrücker
Numerische Methoden der Plasmaphysik (M16)
TU München
Project Summary
Kinetic solvers for plasma physics are essential to understand plasma turbulence in fusion energy devices. With the emerge of exascale computing, interest in fully kinetic solvers arose in the fusion community. Our group has developed a geometric electromagnetic particle-in-cell solver based on a compatible field discretization and a Poisson time integrator. A prototype implementation in Fortran with an MPI-implementation of the particle part was able to achieve good scaling up to a small number of cores only and the serial performance was hampered by a lack of data locality. Within the scope of the KONWIHR project, we have reimplemented our method based on the exascale computing project AMReX. The AMReX library offers data structures and parallelization concepts for both finite volume and finite difference solvers as well as particles. Based on these facilities, we could achieve an implementation where both the field and the particle parts are parallelized. Moreover, the data locality was improved by particle sorting and tiling of the computational domain as well as an improved layout of the flow of the algorithm to minimize data access. Since the AMReX code targets finite difference and finite volume solvers, we have redesigned our algorithm to use mimetic finite differences instead of compatible finite elements for the fields solver.
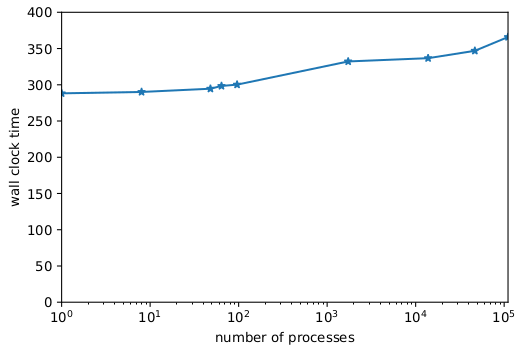
Our new solver shows a very good weak scaling as illustrated in Figure 1 on SuperMUC-NG, with an increase in wall clock time of less than 30% comparing the serial run to a run on 110592 processes (2304 nodes).
The implementation based on the AMReX library also paves the way to multiple further enhancements such as flexible geometry definition through embedded boundaries, efficiency through adaptive mesh refinement, as well as GPU portation of the code through the AMReX GPU backends.