Applicant
Prof. Dr. Wolfgang Wall
Numerische Mechanik
TU München
Project Summary
The KONWIHR project “Matrix-free GPU kernels for complex applications in fluid dynamics” has concentrated on the development and tuning of matrix-free methods for high-order finite element and discontinuous Galerkin discretizations. Our approach relies on expressing the operator evaluation, i.e., matrix-vector product, in iterative solvers by the computation of integrals on the fly with sum factorization techniques on quadrilateral and hexahedral element shapes with an arithmetic intensity of 1.5-10 Flop/Byte. Matrix-free operator evaluation is a promising ingredient for solving fluid dynamics problems on contemporary hardware on the exascale threshold. On the one hand, it enables algorithms several times faster than those relying on the traditional backbone of finite element solvers, the sparse matrix-vector product at 0.16 Flop/Byte. On the other hand, the throughput of the matrix-vector product in terms of unknowns processed per second for higher polynomial degrees is as high or even slightly higher than for linear shape functions. Since higher order methods can provide the same accuracy with fewer unknowns, these algorithmic concepts are enabling technologies for high Reynolds number flows in complex geometries with their large range of active scales and thus extremely high resolution needs.
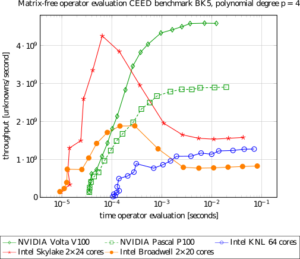
In the finite element and discontinuous Galerkin community, the node-level performance had previously not received much attention, despite being particular interesting both in terms of memory transfer optimizations and arithmetic optimizations due to the arithmetic intensity in the same range as the machine balance of CPUs and GPUs at 6-16 Flop/Byte. Our work has closed this gap, with a particular emphasis on the performance of multigrid solvers on the NVIDIA Pascal and Volta GPUs targeting what is often the dominating algorithmic part in fluid dynamics, the pressure Poisson equation. Furthermore, we have developed new performance models for operator-evaluation on cache-based CPUs and compared the run time of matrix-free operator evaluation on an NVIDIA Volta V100 GPU versus the 2×24 core Intel Xeon Skylake-SP processors used in SuperMUC-NG. Our analysis has shown that the CPU processes more unknowns per second than the GPU in the latency-sensitive regime at small problem sizes. However, while the GPU can increase throughput for larger problem sizes due to the massive parallelism, throughput on the CPU actually decreases because the data must be fetched from the slow RAM memory, rather than the fast caches for smaller sizes. This demonstrates that the GPU would be 2x-3x more energy-efficient for larger problem sizes. The main deficit of the CPU is its main memory bandwidth, showing that additional memory-compression strategies must be developed for SuperMUC-NG with its Skylake processors in the future.

