Applicant
Dr. Martin Kronbichler
Prof. Dr.-Ing. Wolfgang A. Wall
Institute for Computational Mechanics
Technical University of Munich
Boltzmannstr. 15
85747 Garching b. München
Project Summary
This KONWIHR project has enhanced the node-level performance and large-scale scalability of the fluid dynamics solver ExaDG as well as the underlying finite element library deal.II. The solver ExaDG uses high-order discontinuous Galerkin methods for spatial discretization and matrix-free operator evaluation for the iterative solution of linear systems, which are among the most efficient methods for incompressible flows at moderate to high Reynolds numbers. The new developments benefit a range of hardware architectures, but are especially helpful for systems with similar characteristics as the architecture of SuperMUC-NG in terms of arithmetic performance and memory bandwidth.
The major set of new algorithmic developments targeted the node-level performance of our code. More precisely, we aimed to increase the data locality in various central algorithmic ingredients. While matrix-free solvers come with a considerably higher arithmetic intensity than classical matrix-based finite element solvers, our continuous research efforts aiming for a reduction of the arithmetic work in re-computing information on the fly have rendered the methods memory-bandwidth limited on SuperMUC-NG. For the pressure Poisson equation discretized with higher-order discontinuous Galerkin methods, we therefore developed a new Hermite-like polynomial basis that reduces the data access rather than the number of arithmetic operations, and increased the application throughput by 10 to 25 percent. This benefit can be further increased by merging vector operations within the multigrid solvers, such as those for smoothers and level-transfer operations, into the matrix-free loops.
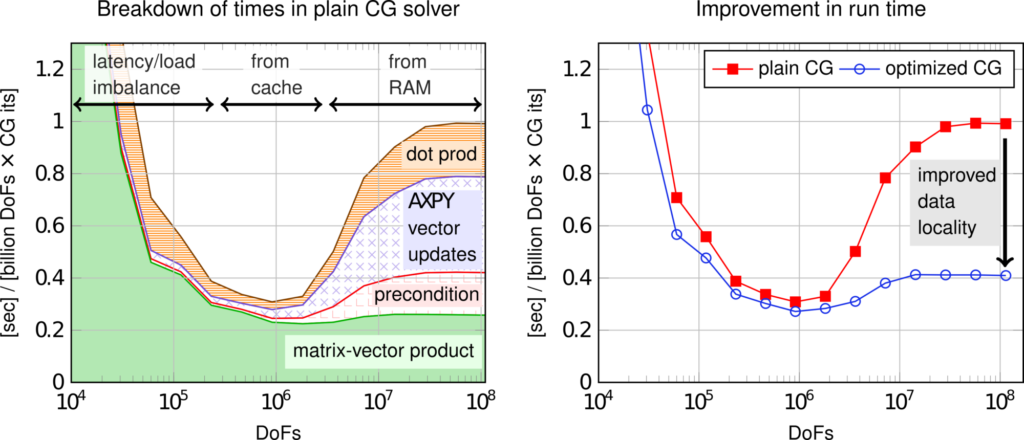
An even more advanced loop fusion approach has been developed for the conjugate gradient solver with a simple diagonal preconditioner, which is important for the viscous sub-step in our flow solver. The motivation for this work is shown by the left panel of the figure below. The optimizations to the matrix-free operator evaluation have rendered the matrix-vector product so fast that the cost of simple vector updates is no longer negligible, at least as long as the vectors need to be primarily fetched from slow RAM memory (the common case in our CFD solvers). Our optimized CG method performs some additional redundant operations with the cheap diagonal preconditioner as well as redundant summations, in order to break the data dependencies in the conjugate gradient method and schedule almost all vector operations near the cell-wise integrals of the matrix-free operator evaluation. This enhanced data locality can speed up the time spent per unknown and CG iteration by a factor of two to three, as seen in the right panel of the figure.
Finally, we also improved the scalability of important setup routines when run on more than 1000 nodes of SuperMUC-NG. These contributions open the way towards more challenging coupled problems with frequent data exchange and updates of the algorithmic components, such as the mesh motion appearing in the simulation of fluid-structure interaction problems with arbitrary Lagrangian-Eulerian methods.